Electric Field
What is an electric field? That’s a complicated question that requires a bit of imagination. So before we jump into an answer, let’s look to the Earth’s gravitational field for general answers about fields.
Gravitational Field
Gravitational Force
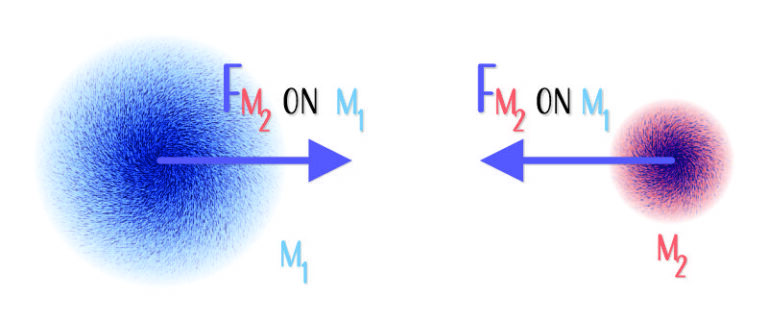
When we think of gravity, we tend to think of common objects falling towards Earth’s surface. But that is only half of an interaction. We do not tend to think about the Earth’s attraction to everyday objects because the Earth’s acceleration towards that object is imperceptibly small.
And we certainly don’t think about everyday objects exerting a gravitational force on one another, and that is because the gravitational interaction is so weak we have personally never witnessed it. Outside of carefully-designed experiments, you generally need an astronomically-sized object to generate the forces required to observe an interaction.
Do the Math
Use the gravitational mass of two objects, the constant of proportionality G, and the distance between the objects’ centers of mass, we can find the gravitational force of attraction between the objects. To do the math properly, we should consider the mass and exact location of every oil and mineral deposit, every rock, every wave, every person, and every other object in the Earth and on the surface. But that is too much work, so we assume a homogenous sphere.
Newton’s law of universal gravitation provides the attractive force for the interaction between Earth (⊕) and some arbitrary object.
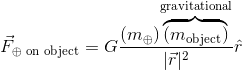
The effects of the force of attraction between the earth and an object on the surface require Newton’s 2nd law and the object’s inertial mass.
Einstein’s theory of relativity and all experiments performed to date have shown an equivalence between inertial and gravitational mass, so we can justify setting them equal.
And to further simplify things, we might as well substitute that radius of the Earth into the equation as our separation distance, r, since almost all human activity lies within a few dozen kilometers of the surface of the Earth. Then we can solve the equations for acceleration at or near the surface.
The answer that comes out is much easier to work with than the previous equations and is independent of the object’s mass.
All humans near the surface of the Earth, from miners below the surface to pilots in commercial airplanes experience this same acceleration towards the center of the Earth.[1] It is far easier to work with g=9.8(m/s2)than to go through this derivation every time you want to determine the acceleration of a new object. Since the mass of the object always cancels out of the equation, the acceleration will always be around g=9.8(m/s2).
The Earth is not homogeneous, and it’s not a sphere. It is an ellipsoid with mountains and valleys, oil and mineral deposits, oceans, and all sorts of unique features. The gravitational field surrounding the Earth is non-uniform.
Suppose you dropped an object at 800 equally spaced locations around the globe and drew an arrow at that location to indicate the direction of acceleration. In that case, you might end up with the image below.

This three-dimensional vector field shows the direction and magnitude of acceleration at equally spaced points near the surface of the Earth. The rainbow colors indicate the relative difference from average acceleration, with redder arrows indicating greater acceleration magnitude near the poles and purple indicating lower acceleration magnitude near the equator.
Vector Fields
If the length of the arrow is proportional to the magnitude of acceleration, the arrow becomes a vector. Mathematically, the collection of vectors is a vector field, and a value is defined everywhere in the region, not just the locations defined by arrows.
Fields are mathematical constructs that show how an object’s properties change in a two or three-dimensional region.
Since the vector-field we used in our example is due to gravity, another name for the collection of arrows is a gravitational field.
Next questions
You need to put an object at a point in a gravitational field to witness an acceleration; if there’s no object, there’s no acceleration, so what gives! If there is no second object, is there something there in the space or not? And what, if anything, happens in the space on the far side of the charged particles? What happens in the physical space around a single charged particle? Does the simple presence of a charged object perturb space in some way? This is maddening! We’ll get answers to some of these questions in the next article!
In the meantime, here’s another gravity vector field image for you pin to the wall of your office.




